1 - Introdução
Chama-se seqüência ou sucessão numérica, a qualquer conjunto ordenado de números reais ou complexos. Assim, por exemplo, o conjunto ordenado A = ( 3, 5, 7, 9, 11, ... , 35) é uma seqüência cujo primeiro termo é 3, o segundo termo é 5, o terceiro termo é 7 e assim sucessivamente.
Uma seqüência pode ser finita ou infinita.
O exemplo dado acima é de uma seqüência finita.
Já a seqüência P = (0, 2, 4, 6, 8, ... ) é infinita.
Uma seqüência numérica pode ser representada genericamente na forma:
(a
1, a
2, a
3, ... , a
k, ... , a
n, ...) onde a
1 é o primeiro termo, a
2 é o segundo termo, ... , a
k é o k-ésimo termo, ... , a
n é o n-ésimo termo. (Neste caso, k <>
Por exemplo, na seqüência Y = ( 2, 6, 18, 54, 162, 486, ... ) podemos dizer que a
3 = 18, a
5 = 162, etc.
São de particular interesse, as seqüências cujos termos obedecem a uma lei de formação, ou seja é possível escrever uma relação matemática entre eles.
Assim, na seqüência Y acima, podemos observar que cada termo a partir do segundo é igual ao anterior multiplicado por 3.
A lei de formação ou seja a expressão matemática que relaciona entre si os termos da seqüência, é denominada
termo geral.
Considere por exemplo a seqüência S cujo termo geral seja dado por a
n = 3n + 5, onde n é um número natural não nulo.
Observe que atribuindo-se valores para n, obteremos o termo a
n (n - ésimo termo) correspondente.
Assim por exemplo, para n = 20, teremos
a
n = 3.20 + 5 = 65, e portanto o vigésimo termo dessa seqüência (a
20) é igual a 65.
Prosseguindo com esse raciocínio, podemos escrever toda a seqüência S que seria:
S = ( 8, 11, 14, 17, 20, ... ).
Dado o termo geral de uma seqüência, é sempre fácil determiná-la.
Seja por exemplo a seqüência de termo geral a
n = n
2 + 4n + 10, para n inteiro e positivo.
Nestas condições, podemos concluir que a seqüência poderá ser escrita como:
(15, 22, 31, 42, 55, 70, ... ).
Por exemplo:
a
6 = 70 porque a
6 = 6
2 + 4.6 + 10 = 36 + 24 + 10 = 70.
2 - Conceito de Progressão Aritmética - PA
Chama-se Progressão Aritmética – PA – à toda seqüência numérica cujos termos a partir do segundo, são iguais ao anterior somado com um valor constante denominado razão.
Exemplos:
A = ( 1, 5, 9, 13, 17, 21, ... ) razão = 4 (PA crescente)
B = ( 3, 12, 21, 30, 39, 48, ... ) razão = 9 (PA crescente)
C = ( 5, 5, 5, 5, 5, 5, 5, ... ) razão = 0 (PA constante)
D = ( 100, 90, 80, 70, 60, 50, ... ) razão = -10 ( PA decrescente)
3 - Termo Geral de uma PA
Seja a PA genérica (a
1, a
2, a
3, ... , a
n, ...) de razão r.
De acordo com a definição podemos escrever:
a
2 = a
1 + 1.r
a
3 = a
2 + r = (a
1 + r) + r = a
1 + 2r
a
4 = a
3 + r = (a
1 + 2r) + r = a
1 + 3r
.....................................................
Podemos inferir (deduzir) das igualdades acima que: .............. a
n = a
1 + (n – 1) . r
A expressão
an = a1 + (n – 1) . r é denominada termo geral da PA.
Nesta fórmula, temos que
an é o termo de ordem
n (n-ésimo termo) ,
r é a razão e
a1 é o primeiro termo da Progressão Aritmética – PA.
Exemplos:
Qual o milésimo número ímpar positivo?
Temos a PA: ( 1, 3, 5, 7, 9, ... ) onde o primeiro termo a
1= 1, a razão r = 2 e queremos calcular o milésimo termo a
1000. Nestas condições, n = 1000 e poderemos escrever:
a
1000 = a
1 + (1000 - 1).2 = 1 + 999.2 = 1 + 1998 = 1999.
Portanto, 1999 é o milésimo número ímpar.
Qual o número de termos da PA: ( 100, 98, 96, ... , 22) ?
Temos a
1 = 100, r = 98 -100 = - 2 e a
n = 22 e desejamos calcular n.
Substituindo na fórmula do termo geral, fica: 22 = 100 + (n - 1). (- 2) ;
logo, 22 - 100 = - 2n + 2 e, 22 - 100 - 2 = - 2n de onde conclui-se que - 80 = - 2n ,
de onde vem n = 40.
Portanto, a PA possui 40 termos.
Através de um tratamento simples e conveniente da fórmula do termo geral de uma PA, podemos generaliza-la da seguinte forma:
Sendo a
j o termo de ordem j (j-ésimo termo) da PA e a
k o termo de ordem k ( k-ésimo termo) da PA, poderemos escrever a seguinte fórmula genérica:
aj = ak + (j - k).r
Exemplos:
Se numa PA o quinto termo é 30 e o vigésimo termo é 60, qual a razão?Temos a
5 = 30 e a
20 = 60.
Pela fórmula anterior, poderemos escrever:
a
20 = a
5 + (20 - 5) . r e substituindo fica: 60 = 30 + (20 - 5).r ;
60 - 30 = 15r ; logo, r = 2.
Numa PA de razão 5, o vigésimo termo vale 8. Qual o terceiro termo?
Temos r = 5, a
20 = 8.
Logo, o termo procurado será: a
3 = a
20 + (3 – 20).5
a
3 = 8 –17.5 = 8 – 85 = - 77.
4 - Propriedades das Progressões Aritméticas
Numa PA, cada termo (a partir do segundo) é a média aritmética dos termos vizinhos deste.
Exemplo:PA : ( m, n, r ) ; portanto, n = (m + r) / 2
Assim, se lhe apresentarem um problema de PA do tipo:
Três números estão em PA, ... ,
a forma mais inteligente de resolver o problema é considerar que a PA é do tipo:
(x - r, x, x + r), onde r é a razão da PA.
Numa PA, a soma dos termos eqüidistantes dos extremos é constante.
Exemplo:PA : ( m, n, r, s, t); portanto, m + t = n + s = r + r = 2r
Estas propriedades facilitam sobremaneira a solução de problemas.
5 - Soma dos n primeiros termos de uma PA
Seja a PA ( a
1, a
2, a
3, ..., a
n-1, a
n).
A soma dos n primeiros termos S
n = a
1 + a
2 + a
3 + ... + a
n-1 + a
n , pode ser deduzida facilmente, da aplicação da segunda propriedade acima.
Temos:
S
n = a
1 + a
2 + a
3 + ... + a
n-1 + a
n
É claro que também poderemos escrever a igualdade acima como:
S
n = a
n + a
n-1 + ... + a
3 + a
2 + a
1
Somando membro a membro estas duas igualdades, vem:
2. S
n = (a
1 + a
n) + (a
2 + a
n-1) + ... + (a
n + a
1)
Logo, pela segunda propriedade acima, as n parcelas entre parênteses possuem o mesmo valor ( são iguais à soma dos termos extremos a
1 + a
n ) , de onde concluímos inevitavelmente que:
2.S
n = (a
1 + a
n).n , onde n é o número de termos da PA.
Daí então, vem finalmente que:
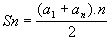Exemplo:
Calcule a soma dos 200 primeiros números ímpares positivos.
Temos a PA: ( 1, 3, 5, 7, 9, ... )
Precisamos conhecer o valor de a
200 .
Mas, a
200 = a
1 + (200 - 1).r = 1 + 199.2 = 399
Logo, S
n = [(1 + 399). 200] / 2 = 40.000
Portanto, a soma dos duzentos primeiros números ímpares positivos é igual a 40000.
Exercícios resolvidos e propostos:
1 - Qual é o número mínimo de termos que se deve somar na P.A. :( 7/5 , 1 , 3/5 , ... ) , a partir do primeiro termo, para que a soma seja negativa?*a) 9
b) 8
c) 7
d ) 6
e) 5
SOLUÇÃO:
Temos:
a1 = 7/5 e r = 1 – 7/5 = 5/5 – 7/5 = -2/5, ou seja:
r = -2/5.
Poderemos escrever então, para o n-ésimo termo a
n:
a
n = a
1 + (n – 1).r = 7/5 + (n – 1).(-2/5)
a
n = 7/5 – 2n/5 + 2/5 = (7/5 + 2/5) –2n/5 = 9/5 –2n/5 = (9 – 2n)/5
A soma dos n primeiros termos, pela fórmula vista anteriormente será então:
S
n = (a
1 + a
n). (n/2) = [(7/5) + (9 – 2n)/5].(n/2) = [(16 – 2n)/5].(n/2)
S
n = (16n – 2n
2) / 10
Ora, nós queremos que a soma S
n seja negativa; logo, vem:
(16n – 2n
2) / 10 <>
Como o denominador é positivo, para que a fração acima seja negativa, o numerador deve ser negativo. Logo, deveremos ter:
16n – 2n
2 <>
Portanto, n(16 – 2n ) < 0
Ora, como n é o número de termos, ele é um número inteiro e positivo. Portanto, para que o produto acima seja negativo, deveremos ter:
16 – 2n <> 16 ou n > 8.
Como n é um número inteiro positivo, deduzimos imediatamente que n = 9.
Portanto, a alternativa correta é a letra A.
2 - As medidas dos lados de um triângulo são expressas por x + 1, 2x , x2 - 5 e estão em P.A. , nesta ordem. O perímetro do triângulo vale:a) 8
b) 12
c) 15
*d) 24
e) 33
SOLUÇÃO:
Ora, se x + 1, 2x , x
2 – 5 formam uma P.A. , podemos escrever:
2x – (x + 1) = (x
2 – 5) – 2x
2x – x –1 + 5 – x
2 + 2x = 0
3x + 4 – x
2 = 0
Multiplicando por (-1) ambos os membros da igualdade acima, fica:
x
2 – 3x – 4 = 0
Resolvendo a
equação do segundo grau acima encontraremos x = 4 ou x = - 1.
Assim, teremos:
x = 4: os termos da P.A . serão: x+1, 2x, x
2 – 5 ou substituindo o valor de x encontrado: 5, 8, 11, que são as medidas dos lados do triângulo. Portanto, o perímetro do triângulo (soma das medidas dos lados) será igual a 5+8+11 = 24.
O valor negativo de x não serve ao problema, já que levaria a valores negativos para os lados do triângulo, o que é uma impossibilidade matemática, pois as medidas dos lados de um triângulo são necessariamente positivas. Portanto, a alternativa correta é a letra D.
3 - UFBA - Um relógio que bate de hora em hora o número de vezes correspondente a cada hora, baterá , de zero às 12 horas x vezes. Calcule o dobro da terça parte de x.Resp: 60
SOLUÇÃO:
Teremos que:
0 hora o relógio baterá 12 vezes. (Você não acha que bateria 0 vezes, não é?).
1 hora o relógio baterá 1 vez
2 horas o relógio baterá 2 vezes
3 horas o relógio baterá 3 vezes
....................................................
....................................................
12 horas o relógio baterá 12 vezes.
Logo, teremos a seguinte seqüência:
(
12,
1, 2, 3, 4, 5, ... , 12)
A partir do segundo termo da seqüência acima, temos uma PA de 12 termos, cujo primeiro termo é igual a 1, a razão é 1 e o último termo é 12.
Portanto, a soma dos termos desta PA será:
S = (1 + 12).(12/2) = 13.6 = 78
A soma procurada será igual ao resultado anterior (a PA em
vermelho acima) mais as
12 batidas da zero hora. Logo, o número
x será igual a
x = 78 + 12 = 90.
Logo, o dobro da terça parte de
x será: 2. (90/3) = 2.30 =
60, que é a resposta do problema proposto.
4 - UFBA - Numa progressão aritmética, o primeiro termo é 1 e a soma do n-ésimo termo com o número de termos é 2. Calcule a razão dessa progressão.Resp: r = -1
SOLUÇÃO:
Temos: a
1 = 1 e a
n + n = 2, onde a
n é o n-ésimo termo.
Fazendo n = 2, vem: a
2 + 2 = 2, de onde vem imediatamente que a
2 = 0.
Daí, r = a
2 – a
1 = 0 – 1 =
-1, que é a resposta procurada.
5 - A soma dos múltiplos positivos de 8 formados por 3 algarismos é:a) 64376
b) 12846
c) 21286
d) 112
*e) 61376
SOLUÇÃO:
Números com 3 algarismos
: de 100 a 999.
Primeiro múltiplo de 8 maior do que 100 = 104 (que é igual a 8x13)
Maior múltiplo de 8 menor do que 999 = 992 (que é igual a 8x124)
Temos então a PA: (104, 112, 120, 128, 136, ... , 992).
Da fórmula do termo geral
an = a1 + (n – 1) . r poderemos escrever:
992 = 104 + (n – 1).8, já que a razão da PA é 8.
Daí vem: n = 112
Aplicando a fórmula da soma dos n primeiros termos de uma PA, teremos finalmente:
S
n = S
112 = (104 + 992).(112/2) = 61376
A alternativa correta é portanto, a letra E.
6 – Determinar o centésimo termo da progressão aritmética na qual a soma do terceiro termo com o sétimo é igual a 30 e a soma do quarto termo com o nono é igual a 60.Resp: 965
SOLUÇÃO:
Podemos escrever:
a
3 + a
7 = 30
a
4 + a
9 = 60
Usando a fórmula do termo geral, poderemos escrever:
a
1 + 2r + a
1 + 6r = 30 ou 2.a
1 + 8r = 30
a
1 + 3r + a
1 + 8r = 60 ou 2.a
1 + 11r = 60
Subtraindo membro a membro as duas expressões em negrito, vem:
3r = 30 , de onde concluímos que a razão é igual a r = 10.
Substituindo numa das equações em negrito acima, vem:
2.a
1 + 8.10 = 30, de onde tiramos a
1 = - 25.
Logo, o centésimo termo será:
a
100 = a
1 + 99r = - 25 + 99.10 = 965
O site da UFMG está disponibilizando em portal 30 opções de livros gratuitos do curso de Licenciatura em Matemática à Distância, os livros de Matemática estão no formato de PDF e podem serem baixados clicando nos respectivos links logo abaixo.
